Name: 
 

Chapter 5 Post Test


 1. 
Select the graph of the function.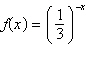

mc001-1.jpg
a.

mc001-2.jpg
d.

mc001-5.jpg
b.

mc001-3.jpg
e.

mc001-6.jpg
c.

mc001-4.jpg
 

 2. 
Use a graphing utility to construct a table of values for the function. Round your answer to two decimal places.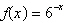

mc002-1.jpg
a.
mc002-2.jpg
b.
mc002-3.jpg
c.
mc002-4.jpg
d.
mc002-5.jpg
e.
mc002-6.jpg
 

 3. 
Sketch the graph of the function.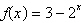

mc003-1.jpg
a.

mc003-2.jpg
d.

mc003-5.jpg
b.

mc003-3.jpg
e.

mc003-6.jpg
c.

mc003-4.jpg
 

 4. 
Write the exponential equation in logarithmic form.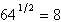

mc004-1.jpg
a.
mc004-2.jpg
b.
mc004-3.jpg
c.
mc004-4.jpg
d.
mc004-5.jpg
e.
mc004-6.jpg
 

 5. 
Write the exponential equation in logarithmic form.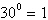

mc005-1.jpg
a.
mc005-2.jpg
b.
mc005-3.jpg
c.
mc005-4.jpg
d.
mc005-5.jpg
e.
mc005-6.jpg
 

 6. 
Use the One-to-One Property to solve the equation for x.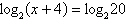

mc006-1.jpg
a.
19
b.
17
c.
18
d.
16
e.
20
 

 7. 
Use the One-to-One Property to solve the equation for x.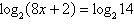

mc007-1.jpg
a.
mc007-2.jpg
b.
mc007-3.jpg
c.
mc007-4.jpg
d.
mc007-5.jpg
e.
mc007-6.jpg
 

 8. 
Rewrite the logarithm as a ratio of natural logarithms.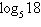

mc008-1.jpg
a.
mc008-2.jpg
b.
mc008-3.jpg
c.
mc008-4.jpg
d.
mc008-5.jpg
e.
None of these
 

 9. 
Rewrite the logarithm as a ratio of natural logarithms.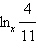

mc009-1.jpg
a.
mc009-2.jpg
b.
mc009-3.jpg
c.
mc009-4.jpg
d.
mc009-5.jpg
e.
None of these
 

 10. 
Rewrite the logarithm as a ratio of common logarithms.

mc010-1.jpg
a.
mc010-2.jpg
b.
mc010-3.jpg
c.
mc010-4.jpg
d.
mc010-5.jpg
e.
None of these
 

 11. 
Use the change-of-base formula to rewrite the logarithm as a ratio of logarithms. Then use a
graphing utility to graph the ratio.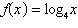

mc011-1.jpg
a.
mc011-2.jpg

mc011-3.jpg
d.
mc011-8.jpg

mc011-9.jpg
b.
mc011-4.jpg

mc011-5.jpg
e.
mc011-10.jpg

mc011-11.jpg
c.
mc011-6.jpg

mc011-7.jpg
 

 12. 
Find the exact value of 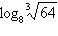mc012-1.jpg without using a calculator.
a.
mc012-2.jpg
b.
mc012-3.jpg
c.
mc012-4.jpg
d.
–1
e.
mc012-5.jpg
 

 13. 
Determine whether the given x-value is a solution (or an approximate solution) of the equation.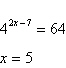

mc013-1.jpg 
a.
No
b.
Yes
 

 14. 
Determine whether the given x-value is a solution (or an approximate solution) of the equation.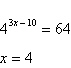

mc014-1.jpg 
a.
No
b.
Yes
 

 15. 
Solve for 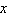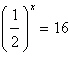mc015-1.jpg.

mc015-2.jpg
a.
2
b.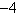
mc015-3.jpg
c.
6
d.
4
e.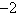
mc015-4.jpg
 

 16. 
Solve for 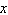mc016-1.jpg. Approximate the result to three decimal places.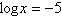

mc016-2.jpg
a.
mc016-3.jpg
b.
0.00001
c.
mc016-4.jpg
d.
mc016-5.jpg
e.
1.609
 

 17. 
Solve the exponential equation algebraically. Approximate the result to three decimal places.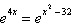

mc017-1.jpg
a.
mc017-2.jpg
b.
mc017-3.jpg
c.
mc017-4.jpg
d.
mc017-5.jpg
e.
mc017-6.jpg
 

 18. 
$6500 is invested in an account at interest rate r, compounded continuously. Find the time required for the amount to triple. (Approximate the result to two decimal places.)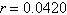

mc018-1.jpg
a.
15.50 yr
b.
14.50 yr
c.
26.16 yr
d.
18.50 yr
e.
17.50 yr
 

 19. 
Solve for x: 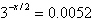mc019-1.jpg. Round to 3 decimal places.
a.
–12.715
b.
9.574
c.
12.715
d.
–4.787
e.
10.518
 

 20. 
Complete the table for the radioactive isotope. Round your answer to two decimal places.

Isotope
Half-life
(years)
Initial Quantity
Amount after 1000 years
mc020-1.jpg
5715
mc020-2.jpg
----
a.
Amount after 1000 years: 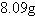mc020-3.jpg
b.
Amount after 1000 years: 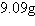mc020-4.jpg
c.
Amount after 1000 years: 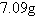mc020-5.jpg
d.
Amount after 1000 years: 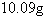mc020-6.jpg
e.
Amount after 1000 years: 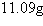mc020-7.jpg
 



 
Check Your Work     Start Over