|
|
|
1.
|
Solve the system by the method of
substitution.
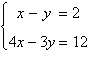
|
|
|
2.
|
Solve the system graphically.
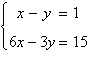
|
|
|
3.
|
Solve the system by the method of elimination and
check any solutions algebraically.
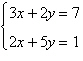
|
|
|
4.
|
Solve the system by the method of
elimination.
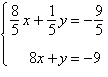
a. | 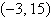 | b. | 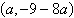 (dependent) (dependent) | c. | 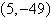 | d. | inconsistent | e. | 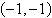 |
|
|
|
5.
|
Find the least squares regression line 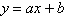 for the points for the points
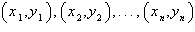
by solving the system for a and
b.
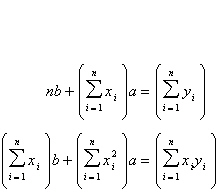
Points: 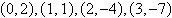
a. | y = 3.93x
–4.21 | b. | y =
2.80x –3.20 | c. | y =
–2.66x +2.80 | d. | y =
–3.47x –4.21 | e. | y =
–3.20x +2.80 |
|
|
|
6.
|
Use back-substitution to solve the system of linear
equations.
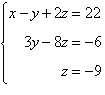
|
|
|
7.
|
Find the equation of the circle 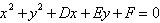 that passes through the points.
that passes through the points.
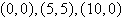
|
|
|
8.
|
Find values of x, y, and 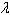 that satisfy the system. These systems arise in certain optimization problems in
calculus, and that satisfy the system. These systems arise in certain optimization problems in
calculus, and 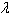 is called a Lagrange multiplier. is called a Lagrange multiplier.
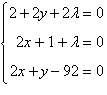
|
|
|
9.
|
A chemist needs 10 liters of a 25% acid solution.
The solution is to be mixed from three
solutions whose concentrations are 10%, 20%, and 50%. How
many liters of each solution will satisfy each condition? Use 2 liters of the 50%
solution.
a. | 2 L of 10%, 7 L of 20%, 1 L of 50%
| b. | 7 L of 10%, 7 L of 20%, 2 L of 50%
| c. | 7 L of 10%, 1 L of 20%, 2 L of 50%
| d. | 1 L of 10%, 2 L of 20%, 7 L of
50% | e. | 1 L of 10%, 7 L of 20%, 2 L of 50%
|
|
|
|
10.
|
Write the form of the partial fraction
decomposition of the rational expression. Do not solve for the constants.
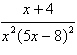
|
|
|
11.
|
Write the partial fraction decomposition of the
rational expression. Check your result algebraically.
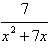
|
|
|
12.
|
Write the partial fraction decomposition of the
rational expression. Check your result algebraically.
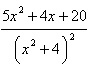
|
|
|
13.
|
Write the partial fraction decomposition of the
rational expression.
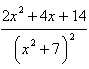
|
|
|
14.
|
Select the correct graph of the
inequality.
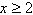
|
|
|
15.
|
Find the consumer surplus and producer
surplus.
Demand 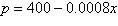
Supply 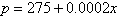
|
|
|
16.
|
Find the minimum value of the objective function
and where they occur, subject to the indicated constraints.
Objective function:
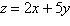
Constraints:
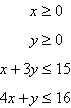
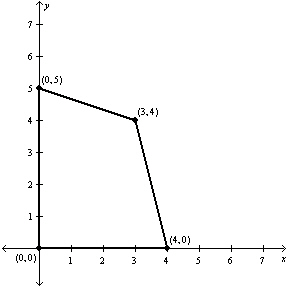
a. | Minimum at 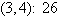 | b. | Minimum at 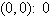 | c. | Minimum at 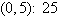 | d. | Minimum at 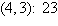 | e. | Minimum at 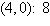 |
|
|
|
17.
|
Select the region determined by the constraints.
Then find the minimum value of the objective function (if possible) and where they occur, subject to
the indicated constraints.
Objective function:
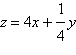
Constraints:
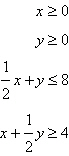
|
|
|
18.
|
Find the maximum value of the objective function
and where they occur, subject to the constraints:
Objective function:
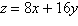
Constraints:
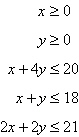
a. | Maximum at 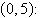 80 80 | b. | Maximum at 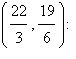 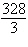 | c. | No maximum | d. | Maximum at 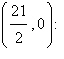 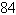 | e. | Maximum at 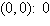 |
|
|
|
19.
|
The linear programming problem has an unusual
characteristic. Select a graph of the solution region for the problem and describe the unusual
characteristic. Find the maximum value of the objective function (if possible) and where they
occur.
Objective function:
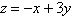
Constraints:
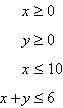
|
|
|
20.
|
An accounting firm has 780 hours of staff time and
272 hours of reviewing time available each week. The firm charges 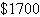 for an audit
and for an audit
and 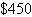 for a tax return. Each audit requires 60
hours of staff time and 16 hours of review time. Each tax return requires 10 hours of staff time and
4 hours of review time. What numbers of audits and tax returns will yield an optimal revenue? What is
the optimal revenue? for a tax return. Each audit requires 60
hours of staff time and 16 hours of review time. Each tax return requires 10 hours of staff time and
4 hours of review time. What numbers of audits and tax returns will yield an optimal revenue? What is
the optimal revenue?
a. | 0 audit
16 tax returns
Optimal revenue: 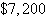 | b. | 13 audits
0 tax
return
Optimal revenue: 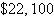 | c. | 16 audits
0 tax return
Optimal revenue: 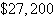 | d. | 0 audit
13 tax
returns
Optimal revenue: 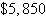 | e. | 10 audits
10 tax returns
Optimal revenue: 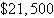 |
|