|
|
|
1.
|
Write the first five terms of the sequence defined
recursively. Use the pattern to write the nth term of the sequence as a function of n.
(Assume that n begins with 1.)
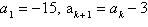
|
|
|
2.
|
Determine whether the sequence is arithmetic. If
so, find the common difference.
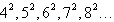
a. | Arithmetic sequence, 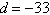 | b. | Arithmetic
sequence, 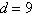 | c. | Arithmetic sequence, 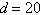 | d. | Arithmetic sequence, 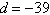 | e. | Not an arithmetic sequence |
|
|
|
3.
|
Find a formula for 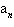 for the
arithmetic sequence. for the
arithmetic sequence.
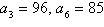
|
|
|
4.
|
Find the sum of the finite arithmetic
sequence.
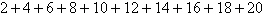
|
|
|
5.
|
Find the sum of the finite geometric sequence.
(Round your answer to three decimal places.)
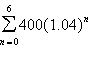
a. | 3,159.318 | b. | 2,166.529 | c. | 444.180 | d. | 2,653.190 | e. | 454.104 |
|
|
|
6.
|
Write an expression for the nth term of the
geometric sequence. Then find the indicated term.
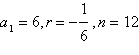
|
|
|
7.
|
Determine whether the sequence is geometric. If so,
find the common ratio.
2, –6, 18,
–54,...
a. | 3 | b. | not
geometric | c. | 2 | d. | –3 | e. | 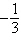 |
|
|
|
8.
|
Match the geometric sequence with its graph from
the choices below.
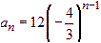
|
|
|
9.
|
|
|
|
10.
|
|
|
|
11.
|
Find a quadratic model for the sequence with the
indicated terms.
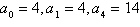
|
|
|
12.
|
Write the first six terms of the sequence beginning
with the given term. Then calculate the first and second differences of the sequence. State whether
the sequence has a linear model, a quadratic model, or neither.
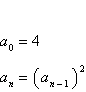
a. | 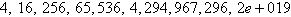
First differences: 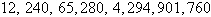 , , 
Second differences: 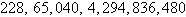 , ,
Neither | b. | 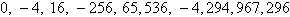
First differences: 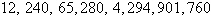 , ,
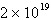
Second differences: 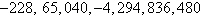 , , 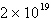
Quadratic | c. | 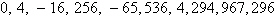
First differences: 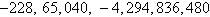 , , 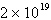
Second differences: 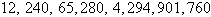 , , 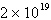
Linear | d. | 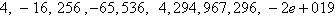
First differences: 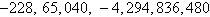 , , 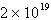
Second differences: 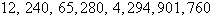 , , 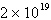
Neither | e. | 
First differences: 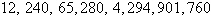 , , 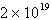
Second differences: 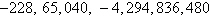 , , 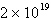
Quadratic |
|
|
|
13.
|
Write the first six terms of the sequence beginning
with the given term. Then calculate the first and second differences of the sequence. State whether
the sequence has a linear model, a quadratic model, or neither.
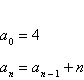
|
|
|
14.
|
Expand the binomial by using Pascal’s
Triangle to determine the coefficients.
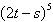
|
|
|
15.
|
Use the Binomial Theorem to expand and simplify the
expression.
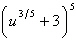
|
|
|
16.
|
You are given the probability that an event will
happen. Find the probability that the event will not happen.
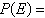 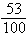
|
|
|
17.
|
There were approximately 32 million unemployed
workers in the United States. The circle graph shows the age profile of these unemployed workers.
What is the probability that a person selected at random from the population of unemployed workers is
45 or older? 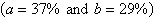
|
|
|
18.
|
The figure shows the results of a survey in which
auto racing fans listed their favorite type of racing. What is the probability that an auto racing
fan selected at random lists NASCAR racing as his or her favorite type of racing? 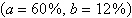
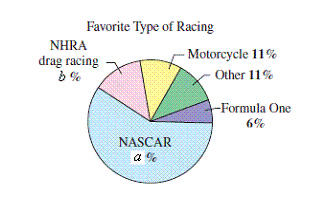
|
|
|
19.
|
In order to be certified, an EMT trainee (EMT
stands for "emergency medical technician") must pass a written examination. A study of 60
trainees is conducted to assess the effectiveness of exam-preparation seminars in reducing the
failure rate. The data are summarized below.| | 0
seminars attended | 1 seminar attended | 2
seminars attended | Total | Passed exam | 7 | 12 | 10 | 29 | Failed
exam | 8 | 15 | 8 | 31 | Total | 15 | 27 | 18 | 60 | | | | | |
Find the probability that the trainee
attended one seminar and passed the exam.
|
|
|
20.
|
|