|
|
|
1.
|
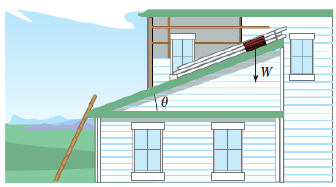
The forces acting on an object weighing X
units on an inclined plane positioned at an angle of 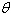 with the horizontal (see
figure) are modeled by with the horizontal (see
figure) are modeled by
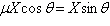
where 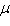 is the
coefficient of friction. Solve the equation for is the
coefficient of friction. Solve the equation for 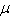 and simplify the
result. and simplify the
result.
|
|
|
2.
|
Use the trigonometric substitution 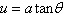 ,
where ,
where 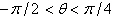 and and 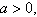 to simplify
the expression to simplify
the expression 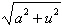 . .
|
|
|
3.
|
Which of the following is equivalent to the given
expression?
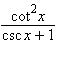
|
|
|
4.
|
Evaluate the following expression.
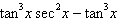
|
|
|
5.
|
Which of the following expression is equivalent
to
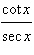
|
|
|
6.
|
Evaluate the following expression.
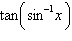
|
|
|
7.
|
Find all solutions of the following equation in the
interval 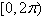 . .
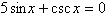
|
|
|
8.
|
Solve the following equation.
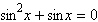
|
|
|
9.
|
Solve the following equation.
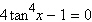
|
|
|
10.
|
Find the expression as the sine of an
angle.
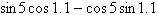
|
|
|
11.
|
Find the expression as the sine or cosine of an
angle.
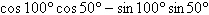
|
|
|
12.
|
Simplify the expression algebraically.
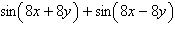
|
|
|
13.
|
Use the figure to find the exact value of the
trigonometric function.
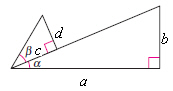
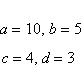
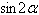
|
|
|
14.
|
Evaluate the expression.
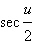
|
|
|
15.
|
Use the figure below to determine the exact value
of the given function.
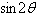
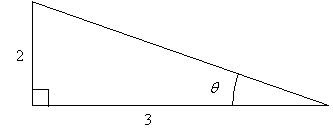
|
|
|
16.
|
Use the figure below to find the exact value of the
given trigonometric expression.
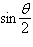
 16 16
30
(figure not necessarily to scale)
|
|
|
17.
|
Use the Law of Sines to
solve the triangle. Round your answer to two decimal places.
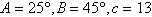
|
|
|
18.
|
Use the Law of Sines to
solve for 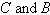 . Round your answer to two decimal
places. . Round your answer to two decimal
places.
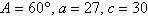
|
|
|
19.
|
Find values for 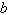 such that
the triangle has two solutions. such that
the triangle has two solutions.
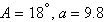
|
|
|
20.
|
Find values for 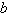 such that
the triangle has no solutions. such that
the triangle has no solutions.
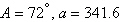
|