|
|
|
1.
|
Use the given values to evaluate (if possible)
three trigonometric functions cotx, secx, cosx.
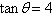 , , 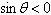
|
|
|
2.
|
Factor; then use fundamental identities to simplify
the expression below and determine which of the following is not equivalent.
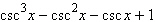
|
|
|
3.
|
Evaluate the following expression.
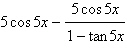
|
|
|
4.
|
Evaluate the following expression.
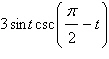
|
|
|
5.
|
Evaluate the expression.
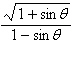
|
|
|
6.
|
Use a graphing utility to graph the
function.
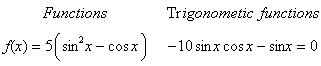
|
|
|
7.
|
A Ferris wheel is built such that the height
h (in feet) above the ground of a seat on the wheel at time t (in seconds) can be
modeled by 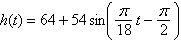 . The wheel makes one revolution every 36
seconds and the ride begins when . The wheel makes one revolution every 36
seconds and the ride begins when 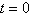 . During the first 36 seconds of the ride, when
will a person, who starts at the bottom of the Ferris wheel, be . During the first 36 seconds of the ride, when
will a person, who starts at the bottom of the Ferris wheel, be 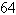 feet above
the ground? feet above
the ground?
a. | 10 seconds and 22 seconds | b. | 10 seconds and 17 seconds | c. | 9 seconds and 27 seconds | d. | 9 seconds and 22
seconds | e. | 9 seconds and 17
seconds |
|
|
|
8.
|
Find the expression as the sine of an
angle.
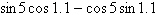
|
|
|
9.
|
Find the expression as the sine or cosine of an
angle.
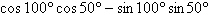
|
|
|
10.
|
A weight is attached to a spring suspended
vertically from a ceiling. When a driving force is applied to the system, the weight moves vertically
from its equilibrium position, and this motion is modeled by
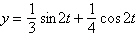
where y
is the distance from equilibrium (in feet) and t is the time (in seconds).
Find the
amplitude of the oscillations of the weight.
|
|
|
11.
|
Use a double-angle formula to rewrite the
expression.
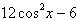
|
|
|
12.
|
Use the sum-to-product formulas to select the sum
or difference as a product.
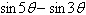
|
|
|
13.
|
Use the sum-to-product formulas to select the sum
or difference as a product.
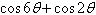
|
|
|
14.
|
Find the exact solutions of the given equation in
the interval 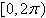 . .
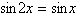
|
|
|
15.
|
Find values for 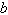 such that the
triangle has no solutions. such that the
triangle has no solutions.
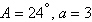
|
|
|
16.
|
Find values for 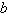 such that the
triangle has one solution. such that the
triangle has one solution.
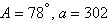
|
|
|
17.
|
Given 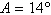 , , 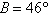 , and , and 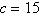 , use the Law of Sines to solve the triangle for the value of b. Round answer to
two decimal places. , use the Law of Sines to solve the triangle for the value of b. Round answer to
two decimal places.
|
|
|
18.
|
After a severe storm, three sisters, April, May,
and June, stood on their front porch and noticed that the tree in their front yard was leaning 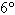 from vertical toward the house. From the porch, which is 98 feet away from the base of
the tree, they noticed that the angle of elevation to the top of the tree was from vertical toward the house. From the porch, which is 98 feet away from the base of
the tree, they noticed that the angle of elevation to the top of the tree was 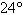 .
Approximate the height of the tree. Round answer to two decimal places. .
Approximate the height of the tree. Round answer to two decimal places.
a. | 47.99 feet | b. | 56.03 feet | c. | 41.91
feet | d. | 45.31 feet | e. | 46.03 feet |
|
|
|
19.
|
Use the Heron’s formula to find the area of
the triangle. Round your answer upto one decimal place.
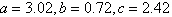
|
|
|
20.
|
Given 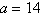 , , 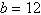 , and , and 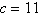 , use Heron's Area Formula to find the area of triangle , use Heron's Area Formula to find the area of triangle 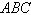 . Round answer
to two decimal places. . Round answer
to two decimal places.
a. | 63.71 sq. units | b. | 54.89 sq. units | c. | 49.12 sq.
units | d. | 51.31 sq. units | e. | 55.42 sq. units |
|