|
|
|
1.
|
Find the angle 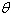 (in radians
and degrees) between the lines. Round your answer to four decimal places for radians and round your
answer to one decimal places for degree. (in radians
and degrees) between the lines. Round your answer to four decimal places for radians and round your
answer to one decimal places for degree.
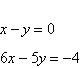
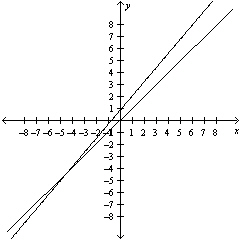
|
|
|
2.
|
Find the angle 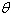 (in radians
and degrees) between the lines. Round your answer to four decimal places for radians and round your
answer to one decimal places for degree. (in radians
and degrees) between the lines. Round your answer to four decimal places for radians and round your
answer to one decimal places for degree.
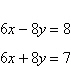
|
|
|
3.
|
Consider a line with slope m and
y-intercept 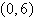 . Select the graph of the distance
between the origin and the line. . Select the graph of the distance
between the origin and the line.
|
|
|
4.
|
Find the standard form of the equation of the
parabola with the given characteristic and vertex at the origin.
Horizontal axis and passes
through the point 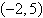
|
|
|
5.
|
The revenue R (in dollars) generated by the
sale of x units of a patio furniture set is given by
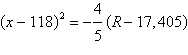 . .
Approximate the number of sales that will maximize revenue.
|
|
|
6.
|
Find the vertex and focus of the parabola.
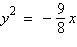
a. | vertex: (0, 0) focus: 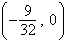 | b. | vertex: (0,
0) focus: 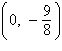 | c. | vertex: 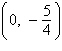 focus: focus: 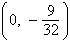 | d. | vertex: (0,
0) focus: 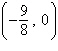 | e. | vertex: 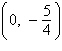 focus: focus: 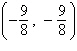 |
|
|
|
7.
|
Find the center and vertices of the ellipse.
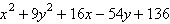 = 0 = 0
a. | center: (3, –8)
vertices: (0, –8), (6, –8) | b. | center: (–8, 3)
vertices: (–11, 3), (–5, 3) | c. | center: (8, –3)
vertices: (7, –3), (9, –3) | d. | center: (8, –3)
vertices: (5, –3), (11, –3) | e. | center: (–8, 3)
vertices: (–9, 3), (–7,
3) |
|
|
|
8.
|
Find the center, vertices and foci of the
hyperbola.
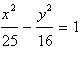
|
|
|
9.
|
Find the standard form of the equation of the
hyperbola with the given characteristics and center at the origin.
Vertices: 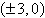 ;
foci: ;
foci: 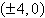
|
|
|
10.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
Vertices: (4,0),(8,0); foci: (0,0),
(10,0)
|
|
|
11.
|
Select the graph of the equation as a circle, a
parabola, an ellipse, or a hyperbola.
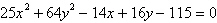
a. | Ellipse | b. | Circle | c. | Hyperbola | d. | Parabola | e. | None of the
above |
|
|
|
12.
|
Find the center and foci of the
hyperbola.
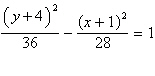
a. | center: (–1, –4), foci: (–9,
–4), (7, –4) | b. | center: (–1,
–4), foci: (–1, –12), (–1, 4) | c. | center: (4, 1), foci: (4, –7), (4, 9) | d. | center: (–4, –1), foci: (–12, –1), (4,
–1) | e. | center: (1, 4), foci: (1, –4), (1,
12) |
|
|
|
13.
|
A point in rectangular coordinates is given.
Convert the point to polar coordinates.
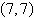
|
|
|
14.
|
Select the graph of the polar equation using
symmetry, zeros, maximum r-values, and any other additional points.
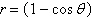
|
|
|
15.
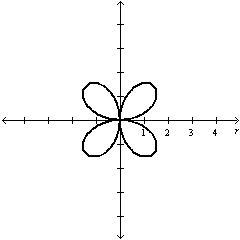
|
Select the graph of the polar equation using
symmetry, zeros, maximum r-values, and any other additional points.
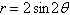
a. | Symmetric with respect to 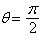 , the polar
axis, and the pole , the polar
axis, and the pole
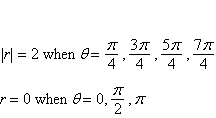
 | d. | Symmetric with respect to 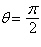 , the polar
axis, and the pole , the polar
axis, and the pole
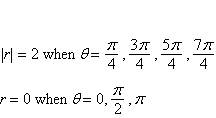
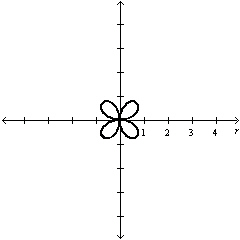 | b. | Symmetric with
respect to 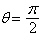 , the polar axis, and the pole , the polar axis, and the pole
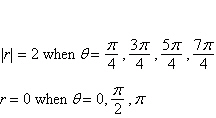
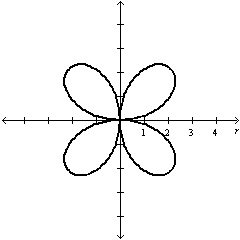 | e. | Symmetric with
respect to 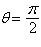 , the polar axis, and the pole , the polar axis, and the pole
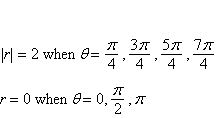
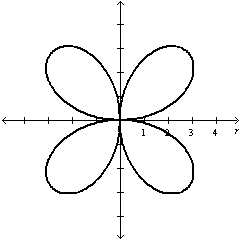 | c. | Symmetric with
respect to 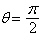 , the polar axis, and the pole , the polar axis, and the pole
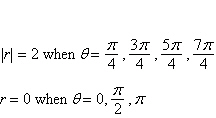
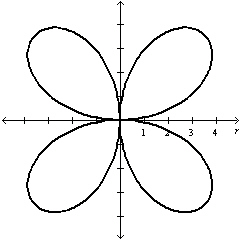 |
|
|
|
16.
|
Select the graph of the polar equation using
symmetry, zeros, maximum r-values, and any other additional points.
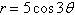
|
|
|
17.
|
Select the graph of the equation.
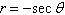
|
|
|
18.
|
Identify the conic and select its correct
graph.
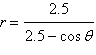
|
|
|
19.
|
Select correct graph to graph rotated
conic.
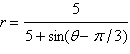
|
|
|
20.
|
Find a polar equation of the conic with its focus
at the pole.
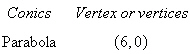
|