|
|
|
1.
|
Find the angle 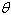 (in radians
and degrees) between the lines. Round your answer to four decimal places for radians and round your
answer to one decimal places for degree. (in radians
and degrees) between the lines. Round your answer to four decimal places for radians and round your
answer to one decimal places for degree.
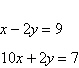
|
|
|
2.
|
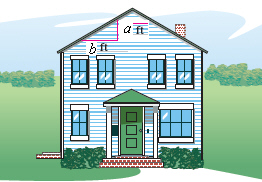
A roof has a rise of 5 feet for every horizontal
change of 7 feet (see figure). Find the
inclination of the roof. Round your answers to one decimal
place.
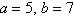
|
|
|
3.
|
Find the standard form of the equation of the
parabola with the given characteristic and vertex at the origin.
Focus: 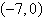
a. | 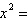 y
y | b. | 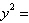 28x
28x | c. | 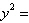 –28x
–28x | d. | 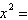 28y
28y | e. | 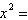 –28y –28y |
|
|
|
4.
|
Find the vertex, focus, and directrix of the
parabola.
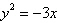
|
|
|
5.
|
Find the standard form of the equation of the
parabola with the given characteristics.
Vertex: 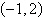 ; focus: ; focus: 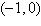
|
|
|
6.
|
Find the center and vertices of the ellipse.
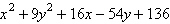 = 0 = 0
a. | center: (3, –8)
vertices: (0, –8), (6, –8) | b. | center: (–8, 3)
vertices: (–11, 3), (–5, 3) | c. | center: (8, –3)
vertices: (7, –3), (9, –3) | d. | center: (8, –3)
vertices: (5, –3), (11, –3) | e. | center: (–8, 3)
vertices: (–9, 3), (–7,
3) |
|
|
|
7.
|
Find the center, vertices and foci of the
hyperbola.
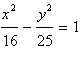
|
|
|
8.
|
Find the standard form of the equation of the
hyperbola with the given characteristics and center at the origin.
Vertices: 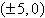 ;
asymptotes: ;
asymptotes: 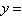 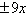
|
|
|
9.
|
Identify the equation as a circle, a parabola, an
ellipse, or a hyperbola.
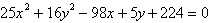
a. | Ellipse | b. | Parabola | c. | Hyperbola | d. | Circle | e. | None of the
above |
|
|
|
10.
|
Select the graph of the equation as a circle, a
parabola, an ellipse, or a hyperbola.
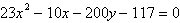
a. | Hyperbola | b. | Circle | c. | Parabola | d. | Ellipse | e. | None of the
above |
|
|
|
11.
|
Find the vertices and asymptotes of the
hyperbola.
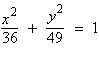
|
|
|
12.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
vertices: 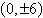 foci: foci: 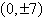
|
|
|
13.
|
Using following result find a set of parametric
equation of conic.
Circle: 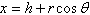 , , 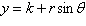
Circle: center: 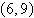 ; radius: ; radius: 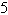
|
|
|
14.
|
Using following result find a set of parametric
equation of conic.
Hyperbola: 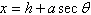 , , 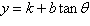
Hyperbola: vertices:
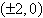 ; foci: ; foci: 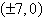
|
|
|
15.
|
Select the parametric equations matching with the
following graph.
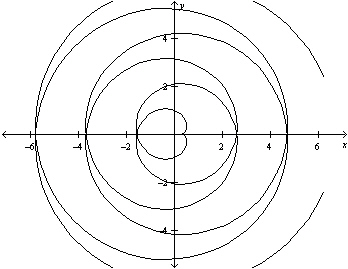
|
|
|
16.
|
A point (a,b) shown in below
graph in polar coordinates is given. Convert the point to rectangular coordinates.
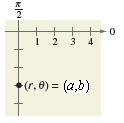
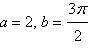
|
|
|
17.
|
Convert the polar equation to rectangular
form.
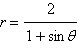
|
|
|
18.
|
Identify the conic and select its correct
graph.
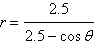
|
|
|
19.
|
Identify the conic and select its correct
graph.
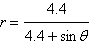
|
|
|
20.
|
Find a polar equation of the conic with its focus
at the pole.
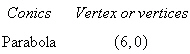
|