Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
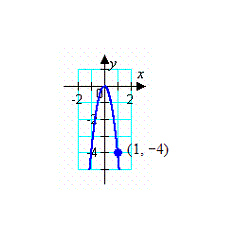
Find the standard form of the equation of the
parabola and determine the coordinates of the focus.
|
|
|
2.
|
Find the standard form of the equation of the
parabola with the given characteristic and vertex at the origin.
directrix: x =
1
a. | x2 =
–4y | b. | y2 = –4x | c. | x2 = 4y | d. | x2 = y | e. | y2 = x |
|
|
|
3.
|
Find the vertex and focus of the parabola.
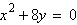
a. | vertex: 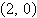 focus:
(0, 0) focus:
(0, 0) | b. | vertex: (0, 0) focus: 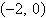 | c. | vertex: (0,
0) focus: 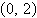 | d. | vertex: (0, 0) focus: 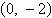 | e. | vertex: 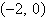 focus: (0, 0) focus: (0, 0) |
|
|
|
4.
|
Find the vertex and focus of the parabola.
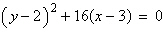
|
|
|
5.
|
Find the vertex and directrix of the
parabola.
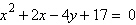
|
|
|
6.
|
Give the standard form of the equation of the
parabola with the given characteristics.
vertex: (–1,
–3) directrix: 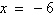
|
|
|
7.
|
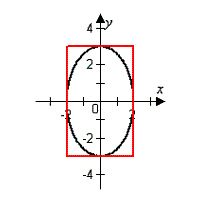
An elliptical stained-glass insert is to be fitted
in a
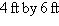
rectangular opening (see figure). Using
the coordinate system shown, find an equation for the ellipse.
|
|
|
8.
|
Find the standard form of the equation of the
ellipse with the following characteristics.
foci: 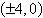 major axis of length:
12 major axis of length:
12
|
|
|
9.
|
Find the center and vertices of the
ellipse.
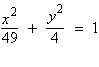
a. | center: (7,
0) vertices: (0, –2), (0,
2) | b. | center: (7,
2) vertices: (–7, –2), (7,
2) | c. | center: (0,
0) vertices: (0, –7), (0,
7) | d. | center: (0,
0) vertices: (–7, 0), (7,
0) | e. | center: (0,
0) vertices: (–2, 0), (2,
0) |
|
|
|
10.
|
Find the center and foci of the
ellipse.
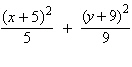
|
|
|
11.
|
Identify the conic by writing the equation in
standard form.
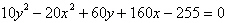
a. | 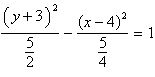 ;
hyperbola ;
hyperbola | b. | 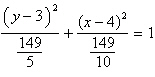 ;
ellipse ;
ellipse | c. | 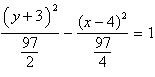 ;
hyperbola ;
hyperbola | d. | 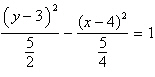 ;
hyperbola ;
hyperbola | e. | 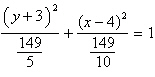 ;
ellipse ;
ellipse |
|
|
|
12.
|
Identify the conic by writing the equation in
standard form.
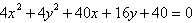
a. | 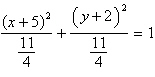 ;
ellipse ;
ellipse | b. | 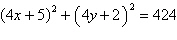 ;
circle ;
circle | c. | 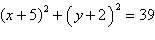 ;
circle ;
circle | d. | 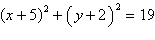 ;
circle ;
circle | e. | 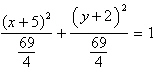 ;
ellipse ;
ellipse |
|
|
|
13.
|
Find the center and vertices of the
ellipse.
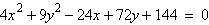
|
|
|
14.
|
Identify the conic by writing the equation in
standard form.
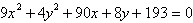
a. | 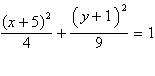 ;
ellipse ;
ellipse | b. | 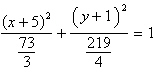 ;
ellipse ;
ellipse | c. | 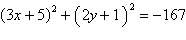 ;
circle ;
circle | d. | 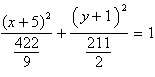 ;
ellipse ;
ellipse | e. | 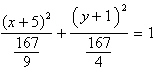 ;
ellipse ;
ellipse |
|
|
|
15.
|
Find the center and vertices of the ellipse.
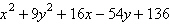 = 0 = 0
a. | center: (3, –8)
vertices: (0, –8), (6, –8) | b. | center: (8, –3)
vertices: (5, –3), (11, –3) | c. | center: (–8, 3)
vertices: (–11, 3), (–5, 3) | d. | center: (–8, 3)
vertices: (–9, 3), (–7, 3) | e. | center: (8, –3)
vertices: (7, –3), (9,
–3) |
|
|
|
16.
|
Find the standard form of the equation of the
ellipse with vertices 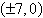 and eccentricity and eccentricity 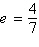 . .
|
|
|
17.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
vertices: 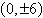 foci: foci: 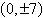
|
|
|
18.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
| vertices: (–2, –4), (–2, 6) | foci: (–2, –5), (–2,
7) | | |
|
|
|
19.
|
Find the standard form of the equation of the
hyperbola with the given characteristics.
| vertices: (0, –1), (10,
–1) | asymptotes: 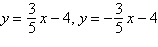 | | |
|
|
|
20.
|
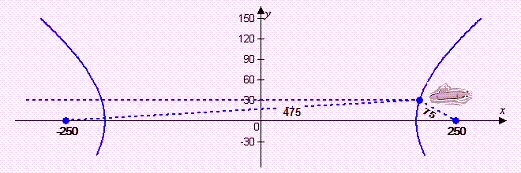
A small submarine is in a narrow underwater canyon
30 feet above the bottom searching for two sunken ships that are known to be 500 feet apart on the
canyon floor. The sonar indicates that one of the wrecks is on the bottom in front of the sub, 475
feet from the nose of the sub, and the other wreck is on the bottom directly behind the sub, 75 feet
from the nose. The difference in the distance from the wrecks to the sub is constant on a hyperbola
having the wrecks as foci.
Assume the two wrecks are positioned on a rectangular
coordinate system at points with coordinates (-250, 0) and (250, 0) as
shown in the figure. Find the x-coordinate of the position of the submarine. (Round to the
nearest whole number, if necessary.)
a. | x = 204 | b. | x = 200 | c. | x =
38,400 | d. | x = 250 | e. | x = 150 |
|