Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Use a graphing utility to solve the system of
equations. Find the solution accurate to two decimal places.
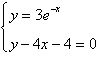
a. | 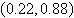 | b. | 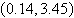 | c. | 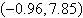 | d. | 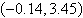 | e. | no real solution |
|
|
|
2.
|
Find the sales necessary to break even (R
– C = 0) for the cost C of producing x units and the revenue R
obtained by selling x units. (Round to the nearest whole unit.)
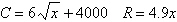
a. | 782 units or 852 units | b. | no real solution | c. | 852
units | d. | 782 units | e. | 831 units |
|
|
|
3.
|
The sales of various types of lawn and garden tools
vary according to the season. At a certain home improvement store, the monthly sales H of
garden hoes (hoes sold per month) declines from July to October whereas the monthly sales of lawn
rakes R (rakes sold per month) increase during this same interval. The sales of these two
items during the calendar months July-October are modeled by the equations:
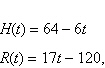
where
t is the month (t = 7 corresponds to July). In which month does the number of
rakes sold equal the number of hoes sold?
a. | July | b. | November | c. | August | d. | September | e. | October |
|
|
|
4.
|
Solve the system by the method of
elimination.
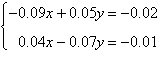
|
|
|
5.
|
Solve using any method.
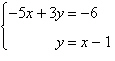
|
|
|
6.
|
An airplane flying into a headwind travels
216 miles in 2 hours and 42 minutes. On the return flight, the distance is traveled in
2 hours. Find the airspeed of the plane and the speed of the wind, assuming that both remain
constant.
a. | plane speed = 94 mph; wind speed =
14 mph | b. | plane speed =
71 mph; wind speed = 14 mph | c. | plane speed =
71 mph; wind speed = 83 mph | d. | plane speed =
109 mph; wind speed = 14 mph | e. | plane speed =
109 mph; wind speed = 101 mph |
|
|
|
7.
|
Find the least squares regression line 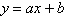 for the points for the points
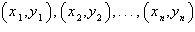
by solving the system for a and
b.
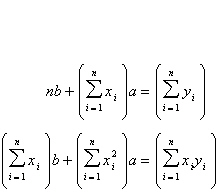
Points: 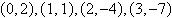 space space
a. | y = –3.47x
–4.21 | b. | y =
3.93x –4.21 | c. | y =
2.80x –3.20 | d. | y =
–2.66x +2.80 | e. | y =
–3.20x +2.80 |
|
|
|
8.
|
Use back-substitution to solve the system of linear
equations.
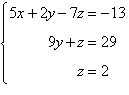
|
|
|
9.
|
Solve the system of linear equations.
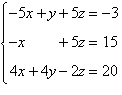
|
|
|
10.
|
Solve the system of linear equations.
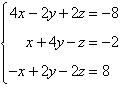
|
|
|
11.
|
Solve the system of linear equations.
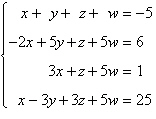
|
|
|
12.
|
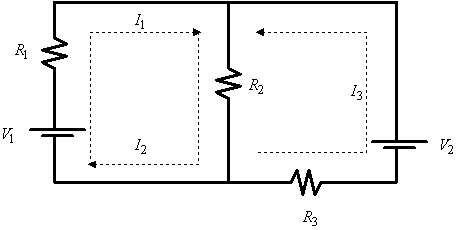
Applying Kirchhoff's Laws to the electrical
network in the figure, the currents I1, I2, and
I3 are the solution of the system
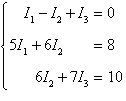
Find the currents.
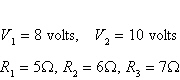
|
|
|
13.
|
Write the form of the partial fraction
decomposition of the rational expression. Do not solve for the constants.
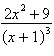
|
|
|
14.
|
Write the partial fraction decomposition of the
rational expression.
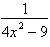
|
|
|
15.
|
Write the partial fraction decomposition of the
rational expression.
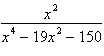
|
|
|
16.
|
Sketch the graph of the inequality.
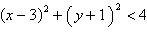
|
|
|
17.
|
Use a graphing utility to graph the inequalities.
Shade the region representing the solution set of the system.
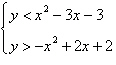
|
|
|
18.
|
Derive a set of inequalities to describe the
region.
|
|
|
19.
|
Find the minimum and maximum values of the
objective function and where they occur, subject to the indicated constraints. (You should graph the
feasible solutions on the grid below before you attempt to find the minimum and maximum
values.)
| Objective function: | | | Constraints: | |  | |
|
|
|
20.
|
An investor has $150,000 to invest in two types of
investments. Type A pays 5% annually and type B pays 6% annually. To have a well-balanced portfolio,
the investor imposes the following conditions. At least one-third of the total portfolio is to be
allocated to type A investments and at least one-third of the portfolio is to be allocated to type B
investments. What is the optimal amount that should be invested in each investment?
a. | $150,000 in type A (5%), $0 in type B
(6%) | b. | $50,000 in type A (5%), $100,000 in type B
(6%) | c. | $100,000 in type A (5%), $50,000 in type B
(6%) | d. | $0 in type A (5%), $150,000 in type B
(6%) | e. | $60,000 in type A (5%), $90,000 in type B
(6%) |
|